| |
|
Abstract
An 'Integrated Computer Art System' is described which offers the computer
artist, illustrator and designer a much wider range of 2D manipulations
than in conventional paint systems. The system allows non-programmers
to explore a range of techniques based on computer geometries and algorithms,
including certain types of fractals, in an interactive fashion, while
still giving full control down to the pixel level. The system is under
development, but already shows potential for generating new computer imagery
not belonging to the now 'conventional' world of 3D photo-realism.
Introduction
Computer graphics has long been associated with 3D scene simulation, with
increasing compute- power devoted to the techniques of photo-realism.
For the artist, illustrator and graphic designer these methods have limited
use, and they have found the 2D paint system, with all its limitations,
to be more suited to their budgets, needs and abilities. Paint systems
have a well established nature by now, and do not receive the intensive
research effort that photo- realism is still receiving. In my proposed
'Integrated Computer Art System' (ICAS) I am trying to redress the balance
by extending the paint system concept with an increased functionality
that addresses the needs of the non-programming computer artist and designer.
ICAS, in brief, provides a mixture of paint and object-oriented techniques
with additional features including pattern-making, tesselations and interactive
fractals. The range of facilities have been selected by a careful consideration
of what the computer can offer to the artist and designer working in two
dimensions, based on a range of old and 'new' geometries. The system can
also be used to create three dimensional imagery, but not based on the
usual computing techniques of photo- realism. These are too restricting
to the artist, for whom a personal feel for depth, light, shade and perspective
is what gives their work a unique character.
1) The concepts behind ICAS
In a paper entitled Towards an Integrated Computer Art System (King 1987) I outlined the basis for ICAS,
building on my PhD research (King 1986), while this paper presents the results
of implementing some of those proposals. The PhD thesis concluded that
the computer provides for a range of new media in the visual arts, and
that their user interfaces are an essential part of the media. In the
thesis I developed a taxonomy of computer art media, and some new terms
which describe concepts that I feel are important in this area, and I
will briefly summarise these here.
The first distinction that I have made is between interactive and
scripted systems. In interactive systems the user is not required
to program the system, and most of the image-making involves a high level
of hand-eye feedback, as in a paint system. Scripted systems, in contrast,
imply the creation of a program script, usually text-based, and its subsequent
execution for the realisation of the imagery. Feedback is thus through
a write - execute - rewrite cycle.
The creation of imagery in either type of system is by synthesis from
primitives, except where image processing or equivalent techniques are
used, in which case a degree of image analysis is also needed. The concept
of synthesis from primitives is a very important one in this context,
and is what makes art and design applications of computers unique. Most
computing applications revolve around information retrieval and analysis,
with the reduction of a large data base into a few concise conclusions
a frequent goal. Alvey Ray Smith (1984) recognised this
when he coined the term 'data base amplification' for the techniques behind
a range of computer generated imagery. The creative and synthetic aspects
of computer art and design systems has not received a large amount of
attention however, and the concepts that I am introducing here should
help to make a more detailed discussion of these applications possible.
In the context of synthesis from primitives I make a second important
distinction: between arbitrary and algorithmic synthesis
from primitives, and indeed much of what follows depends on this distinction.
Arbitrary synthesis from primitives involves a sequence of operations
on the medium that derive from the artistic whim or intuition of the user
- the machine has no 'understanding' of the sequence or control over it.
Algorithmic synthesis involves a sequence of operations governed by a
set of rules that are communicated to the machine and encapsulated in
a machine-executable algorithm. As a simple example the incorporation
of set or coloured pixels following a free-hand curve in a paint system
is arbitrary, while the incorporation of pixels in a (Bresenham) straight
line is algorithmic. One of the challenges of any art medium is the balance
between algorithmic and arbitrary techniques, and I believe it to be especially
so with computer art. In looking at algorithms used by computer artists
and computer graphics researchers since the sixties to generate imagery,
I have realised that these can all be considered as embodiments of different
types of geometry. Looking more closely at these algorithms or geometries,
it seemed that they could conveniently be classified as 'classical' or
'recursive' geometries, and I have listed a 'computer artist's geometrical
toolkit' under these two headings:
The Computer Artist's Geometrical Toolkit
classical GEOMETRIES
· geometries of parallel lines, triangles, rectangles and polygons
· the conic sections: circle, ellipse, parabola and hyperbola
· nets, bands and tesselations
· non-recursive functions
· Lissajou's figures, cardioids and cycloids
· parametric curves
RECURSIVE GEOMETRIES
· iterative functions (recurrence relations)
· random numbers
· recursive patterns
· fractals and graftals
· particle systems
· growth models
· linear and array grammars
· Markov chains
2) Proposed structure of ICAS and progress to date
The proposed structure of ICAS, outlined in King (1987), was a two-level
system, with an object-oriented or drafting level from which one could
'descend' into a paint level. The drafting level was to provide the usual
object-oriented manipulations, but greatly extended in terms of pattern-making,
tesselations and fractals (recursively substituted shapes). The paint
mode allows for pixel-editing of the output from the drafting mode, raster-based
cut and paste, and more gestural and expressive free-hand work.
In the object-oriented or drafting mode the intention was to implement
a wide range of the geometries listed above in the toolkit'. However,
because one can never anticipate all the possible needs of the user, and
because some geometries are difficult or clumsy to control interactively,
it is intended that ICAS should include a scripted component, which would
manipulate the image through the creation of small 'scripts' or programs.
Development effort so far has concentrated on the integration of a drafting
medium and a paint system. The drafting aspect has allowed for a comprehensive
range of manipulations not easily provided for in paint systems, and also
the implementation of the sophisticated pattern-making facilities, and
some interactive fractals. The system is written in C and runs on IBM
PC compatibles driving an Io Research Ltd 8 bit per pixel frame store.
The data structure for the drafting mode is a doubly-linked list of nodes,
each containing a field identifying the primitive (line, poly-line, rectangle,
filled rectangle, circle etc.), and fields containing the variables of
instantiation (position, size and colour). The sequence of the linked
list determines the order of drawing, so that for the user to change the
layering the sequence has to be changed by changing the pointers in the
list. Superimposed on the list is a tree-structure reflecting the hierarchy
that the user imposes on the drawing by creating groupings. The tree-structure
is implemented using grouping nodes that are pointed to by the elements
in the group, and that point back in turn to the elements. The group nodes
also contain information on the extents of the group. An individual group
is manipulated by recursively descending its structure until primitives
are reached.
3) Work-table philosophy
Normally in a paint system all the user's input is stored as a modification
to the array of pixels in a frame buffer, and recovery from the latest
modification is only possible if multiple picture planes are available
(these are expensive and give only limited recovery). Scaling up or down
results in a sampling effect and picture degradation, and hence the full
screen tends to be in use for the image in a paint system. Whatever the
resolution, the user is unlikely to want to give up portions of the screen
'real-estate' to menus, palettes, and icons representing various 'tools'.
These tend to be stored off-screen and blitted onto the screen when required.
This means that spare frame-buffer capacity is required for interactive
systems, and is of course expensive. One of the tricky parts of designing
a paint system on a limited budget, is that often there is little spare
memory.
With an object-oriented or drafting system the problems of scaling up
and down are reduced because of the underlying (vector) description of
the picture. In the design of ICAS I have therefore used only some 80%
of the screen for the image in drafting mode, while using the entire screen
for paint mode. The advantage of working in the drafting mode is that
all the tools are at hand, as illustrated in Fig. 1.
Fig. 1 Screen layout of the ICAS 'work-table'
I call this a 'work-table' approach, because it more closely parallels
a traditional artist's work table, on which one would have to hand brushes,
paints, geometrical instruments and so on. The paint system approach of
blitting up the palette and menus for every single change of colour, brush
and operation is a bit like keeping all these items in a drawer under
your table, with the added complication that opening the drawer obscures
part of the art-work! This is not to be taken as a criticism of windows
in general; it is just an awkward way to work in this particular application.
Coming back to the work-table philosophy, the work area can in fact be
used to store many motifs, scraps of design and so on. The ability to
reduce a fragment down and place it in a corner for later use adds greatly
to the power of the system. While the work table is useful in the construction
of an image, it is a nuisance in that the shapes and colours in the menus
and palettes are distracting from the overall composition and effect of
the created image. Artists get round this by pinning a work in progress
to a blank wall where one can more easily judge the composition. In ICAS
this need is taken into account by a facility that removes the surrounding
menus and palettes and re-draws the image to full scale - as it would
be seen on exit to paint mode. A press of a key then returns the user
to the work table with the reduced image for further manipulation. One
would typically go in and out of the work table a number of times in the
creation of a finished product, in order to judge its progress.
4) Design and motif creation
The basic techniques while in drafting mode are similar to those found
in Macdraw - a drafting system for the Apple Macintosh. The common techniques
of rubber-banding, dragging, and echoing the selection of an item by highlighting
are provided, along with a method for capturing items for manipulation
as a group. Because the palette is always visible, smooth shaded polygons
can be easily created by selecting a new colour between vertices. Flood-fills
are provided, and can be individually deleted by traversing a stored list
of them which highlights them in turn. Figures 2 to 9 show the sequence
of creation of some images, and also illustrates the range of imagery
that the system is capable of. Some of the images contain lines that have
been roughened by a function provided within the fractal menu (described
later).
 |
Fig.
2
First part of a design created using mirror, rotate and copy |
 |
Fig.
3
Design reduced and rotated and more elements added |
 |
Fig.
4
A series of roughened lines are created |
 |
Fig.
5
The previous designs are combined using cut and paste, and free-hand
elements added in paint mode |
|

|
Fig.
6
First stage of a design using shaded polygons |
|

|
Fig.
7
The polygons are grouped as a whole, scaled, mirrored and rotated,
and other elements added |
|

|
Fig.
8
The final image cut and pasted in paint mode |
|
|
Fig.
9
Mostly drafting techniques are used in this abstract composition |
5) Pattern-making
I regard pattern-making as one of the classical computer geometries, and
an obvious area for exploitation by computers in art and design. At present
various arrangements of motifs can be displayed, based loosely on a classification
in MacGregor and Watt (1984).
The user designs a motif, usually to a large a scale as possible, and
then scales it down for repeating. Because of the data-structure underlying
the motif the scaling down can be safely performed, secure in the knowledge
that it will scale up perfectly. The work-table philosophy comes into
play again with pattern-making, because only the currently selected grouping
is patterned. The pattern covers the entire screen, the work-table at
first disappearing On the work-table can be any number of motifs and scraps
of design, and of course these all re-appear on return to drafting mode.
Figure 10 shows the ICAS work-table with some motifs and the following
figures show some sample patterns.
|
|
Fig.
10
ICAS work-table with some motifs for patterning |
|

|
Fig.
12
A combination of patterns |
The system has been used by myself and a few students so far, and it is
surprising how fast one can experiment with different motifs and groupings.
Important elements of pattern-making are rapidly made apparent: the difference
of the final effect with the same motif but with different groupings, and
for any given motif and grouping the arising of emergent forms. These are
shapes created by the gaps between the elements of the motif, and also the
longer thrusts of pattern, which range from harmonious to disturbing in
their overall effect.
Tesellations are not yet implemented, but will again be done at the drafting
level. A tessellation differs from the patterns created through the 17 network
groups in a few essential ways. The key to a tessellation is its outline,
not just its orientation. One can think of a tessellation as consisting
of a plane covered with identical blank tiles, whose outlines fill the plane
without gaps, and whose outlines mark out the image. A form that tessellates
may vary from a rectangular tile to the intricate figurative shapes of Escher,
and may or my not be decorated with motifs. If the form for tessellation
is decorated with a motif there is no requirement that the motif should
interlock - it is just the outline that is important. Figure 13 shows the
basis on which ICAS will provide interactive tesselations. As with patterns
the tessellation will be generated full-screen for exit to paint mode, or,
on return to the work-table, the complete tessellation can be incorporated
into the data-structure for subsequent manipulation.
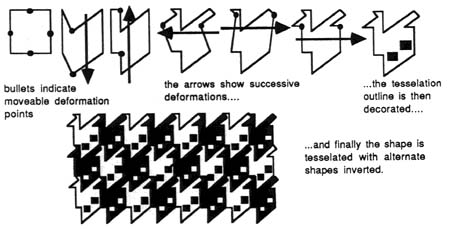
Fig. 13 Interactive
tesselations
6) Interactive fractals
All the previous facilities so far described are based on what I have
called the classical geometries. I have also introduced some recursive
geometries into the system with the provision of some simple fractals.
These are based on the recursive substitution of a collection of line
segments (called the generator) into another collection of line segments
(initiator). At its simplest this is provided by a function called roughen
which uses a simple built-in generator consisting of 3 line segments.
More interesting fractals can be created by the use of user-defined generators
however. As with pattern-making and tesselations the system 'goes out'
to full screen to draw the selected fractalised initiator. The resulting
image depends on the sense of both initiator and generator - i.e. whether
they are drawn clockwise or anticlockwise, leading in the case of the
Von Koch snowflake to the normal or anti- snowflake (see
Mandelbrot, 1982). The generated fractal image can
be 'incorporated' on return to the work-table, for
manipulation in ways already described. Figure 14 shows some examples.
|

|
Fig.
14
Fractal trees cut and paste with recursive rectangles |
As with most
algorithmic synthesis from primitives, once the degree of 'data base amplification'
goes over a certain (fairly low) level, the results (first time) are unpredictable,
though deterministic. The nature of the results can be anticipated with
experience, and it is exactly this experience that ICAS can so rapidly
provide to the artist and designer, both with classical and recursive
techniques.
7) Exit to Paint
On 'exit to paint' the palettes and menus are removed and the image drawn
full-scale, or, in the case of patterns, tesselations and fractals, the
current selection only is 'patterned out' to full size. The image is now
manipulated at a paint level, with the normal low level of editing. Colour
and look-up table manipulation is provided, and indeed the paint component
of ICAS is full- functioned enough to be sufficient for the needs of many
artists. I have found with some of my students that both classical and
recursive geometries hold little interest for them at first; they find
the expressive capabilities of TV resolution 8-bit painting quite sufficient,
and sufficiently different from conventional media to be exciting. However,
the point of ICAS is to extend the paint system to include techniques
that are unique to the computer, either because the technique allows increases
of orders of magnitude in speed of execution (object-oriented manipulations,
pattern-making and tesselations), or because the technique is in practice
impossible to realise by hand (for example fractals).
8) The next step: constraint-driven geometries
The concept of using constraints to describe geometrical problems to the
computer goes back to Sketchpad, through Smalltalk (Byte 1981) and ThingLab
(Borning 1979) to Greg Nelson's
Juno system (Nelson 1985). I plan to make a constraint-solver
the scripted component of ICAS. I conceive the scripted component of ICAS
to be closely integrated with the rest of the system and to look very
little like a conventional high-level programming language. The ideas
put forward by Greg Nelson and his forerunners will be the starting point,
with the interesting challenge of developing constraint-driven recursive
geometries. Imagery from chaotic functions (one of the recursive geometries
in my classification) could be generated by scripts of a few lines.
Conclusion
ICAS is something like half-way towards fulfilling the original concept
and has already shown interesting results, not just in term of the range
of imagery produced with the system, but also in terms of user interface
design. I believe that the development of such systems, taking place outside
the research thrust into photo-realism in computer graphics, will have
an impact on the visual language of a new generation of artists and designers.
By extending the paint system with increased control over both old and
new geometries, the non-programming artist has direct access to a new
world of imagery.
References
Borning 1979: Borning,
Alan, "Thinglab - a Constraint-Oriented Simulation Laboratory"
SSL- 79-3, Xerox PARC, Palo Alto CA July 1979.
King 1986: King, M.R.,
"Computer Media in the Visual Arts and their User Interfaces"
PhD thesis, Royal College of Art, London 1986.
King 1987: King, M.R.,
"Towards an Integrated Computer Art System" in Earnshaw, R.A.
and Lansdown, R.J., (eds.) "State of the Art in Computer Art and
Animation" conference proceedings, Springer Verlag, 1987.
MacGregor and Watt 1984:
Macgregor, J. and Watt, A., "The Art of Microcomputer Graphics"
Addison-Wesley Publishing Co., 1984.
Mandelbrot 1982: Mandelbrot,
B.B., "Fractals: Form, Chance and Dimension" W.H.Freeman and
Company.
Nelson 1985: Nelson,
G., "Juno, a constraint-based graphics system" Computer Graphics,
Volume 19, Number 3, 1985, pp. 235-243.
Smith 1984: Smith, A.L.,
"Plants, Fractals and Formal Languages" SIGGRAPH 84, pp. 1-10.
|
|



