Published in Proceedings of Digital Creativity Conference, Brighton University, ISBN 1-871966-72-8

3,000 words

Abstract
Computer artists and designers are using increasingly sophisticated software packages in the generation and manipulation of images. Many software tools use complex algorithms with a number of parameters to achieve specific visual results, requiring the user to have some understanding of the algorithm and the way in which the parameters control it. This paper looks at methods for manipulating parameters based on the metaphor of navigating a parameter space.

1. Background
1.1 Algorithmic Image Generation
An algorithm is a kind of recipe, and in this context it is a recipe for generating a computer graphics image, or more generally, for controlling aspects of the image. Computer images in art and design may contain no algorithmic elements, or may be partially or totally determined by algorithms. The algorithmic element will involve some setting up by the artist, and will probably feature some kind of repetitive action carried out by the computer.

1.2 Arbitrary and Algorithmic Synthesis from Primitives
In looking at the work of artists, designers, and animators using computer graphics systems I have found it useful to invent the terms arbitrary and algorithmic synthesis and manipulation of primitives. (I have introduced these terms in previous papers, [1] and [2].) In any computer graphics system one is synthesising an image from primitives, which may range from the pixel to 2D geometrical shapes to 3D solid forms, or one may be manipulating a set of existing primitives, e.g. running a filter over a scanned image. In arbitrary synthesis from primitives the system has no control over the placing and attributes of each primitive: the artist is following their own intuition and reasoning, to which the computer is not party. In algorithmic synthesis from primitives the artist or designer yields up control to some degree by imparting to the computer a set of rules (an algorithm) by which it should incorporate or manipulate successive primitives, which may include a random element. The artist will initiate the starting conditions, and allow the computer to take over.

As well as a range of imagery not realisable through other methods there is also the attraction of serendipity. The photographer knows this for example, as he or she watches an image develop in the dark-room; as does the bronze-caster when the mould is broken and the new-born surface is revealed. In computer graphics an image may slowly develop, or only be made visible after an over-night 'batch' render; even with the promise of ever more powerful systems it seems that there will always be some waiting involved, giving rise to a somewhat addictive sense of anticipation.


2. Examples
2.1 Simple and Complex Algorithms
In using any art and design package a surprising number of elements turn out to be under algorithmic control, albeit simple algorithms. Drawing a straight line in a paint package involves a sophisticated algorithm to place the pixels along the path of the line, even though the outcome is 'simple'. The user usually specifies only the beginning and ending of the line, and the algorithm uses a loop to fill the remaining pixels. The line can have a thickness and style, and be anti-aliased, all of which increase the complexity of the algorithm. The same is true for curves, arcs, circles, rectangles, and so on. Smooth-shaded regions require an algorithm that fills an area with colours usually interpolated between a foreground and a background - often the user can choose the interpolation method. Flood-filling is also an algorithmic form of building up an image. Users usually take these for granted, and only consider the more exotic routines such as filters and inbetweening routines as 'algorithmic'.

Fractals and similar images that are entirely generated from an algorithm have tended to be more the domain of the artist / programmer, though various packages now exist that let the non-programmer use them. The early history of computer art was dominated by those who could program, and the precursors to this algorithmic art were those like Franke and Laposky who used oscilloscopes to display images [3]. Herbert Franke has this to say about mathematically based images [4]:

'If one is engaged, as we are, with an inventory of all mathematical branches and with an interest in visualising all forms that come to light, one can obtain plenty of forms, shapes and structures never seen before - an expansion of our treasury of forms. Many of these forms have considerable aesthetic charm. According to the usual criteria we cannot call them original works of art. But they can be considered elements available for new creations and can be used to develop artworks.'

Whether or not artists do successfully use such elements to directly develop artworks will be for history to judge, but there is no doubt that algorithmic elements feature in nearly all computer-mediated imagery. An understanding of the algorithms and how to control them is therefore important to the computer artist and designer. A taxonomy of such algorithms (a systematising of Franke's 'treasury of forms') is important [5], but in this paper we will focus on the methods for controlling them.

2.2 Chaotic and non-chaotic images
There has been much interest in recent years in fractals and chaotic images, which derive from a range of algorithms with different mathematical bases. Fig. 1 shows an image derived from a so-called 'chaotic' function, chaotic because small changes in the parameters have wildly differing effects on the image. Fig. 2 shows a non-chaotic image that is generated from an inverse-square law function that I have developed to generate textures with a strongly laminar feel.

	Fig. 1 A chaotic image
	Fig. 2 Imagery from the inverse-square law

2.3 Textures: Voss fractals and Marbling
Various kind of computer-generated textures have become important in different types of application, notably 3D visualisation and animation software, but also in 2D paint and draw packages. The images shown in fig. 3 are both generated by a fractal algorithm developed by Richard Voss [6], where the parameters relate to the mathematical components of a sine-based algorithm. Fig. 4 shows a marbling texture generated from an algorithm developed by Ken Perlin [7], which uses parameters such as base and vein colour, vein spacing, vein perturbance, and colour bleed, all of which relate to the visual aspects of real marble.

	Fig. 3 Sine-based imagery
	Fig. 4 Marble texture

3. Navigation Techniques for Parameter Space
3.1 Parameters and Algorithms
If algorithms offer the computer artist new tools for expression and even a new visual language, then manipulating their parameters becomes the vehicle for their exploration. We saw in the last section that an algorithm may closely mimic a natural phenomenon, in which case the parameters will relate to the existing (though perhaps highly specialised) understanding of that phenomenon. Alternatively the algorithm may generate unfamiliar imagery, and have equally unfamiliar parameters.

Parameters are of different types: some may be numerical, some may be yes/no decisions, some may be spatial, i.e. requiring the user to specify a 2D or 3D location, or a length or an area. It is the number of parameters that dictate the ease or difficulty of exploring the algorithm. By analogy with geometry we can say that an algorithm requiring one parameter has a one-dimensional parameter space, one requiring two has a two-dimensional parameter space and so on. The Voss fractal 3D texture generator described earlier has roughly 20 parameters, making for a 20-dimensional parameter space.

3.2 Colour Space
In so-called 'full' colour computer graphics systems the user usually has a choice of colour out of 16.7 million, arising from 256 levels of intensity in the three primaries, red, green and blue. We can then say that we control colour by three parameters, and this is often described in terms of an RGB cube, representing a three-dimensional colour space. In getting at just the colour you want, you 'navigate' through this cube until you find it. A more sophisticated model is the hue, saturation, value model, where the cube is mapped into cone. Artists generally find this easy to work with, as hues readily correspond to the colours of the rainbow, or 'pure' colours, while decreasing saturation is like mixing in white paint, and decreasing value is like mixing in black paint.

Different applications allow different ways of representing the HSV cone on a (flat) computer screen and allowing the user to select colours. These are implemented as colour pickers. For each colour model (RGB, HSV, HLS, etc.) software developers design different colour pickers, though often there may be a system-standard method (on the Mac it is HSV, on Windows it is HLS - hue, lightness, and saturation). See fig. 5 for the Windows standard colour picker.

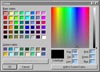Fig. 5 The Windows default colour picker

1. appropriate naming of parameters.
2. visual grouping of parameters.
3. choice of entry method (text, slider, etc.).
4. linking of parameters (e.g. x- and z-parameters).
5. normalising of parameter ranges (e.g. 0 to 100%).
6. quantising of parameter ranges (e.g. jumps of 1 and 10%).
7. recording, commenting on, and retrieving of parameter sets.
8. relating one parameter set to another (evolution).

Another feature that is important with the exploration of parameter space is the concept of a session. The user may spend a period exploring a parameter space, and want to resume at a later date, so it is important that all the parameter sets, or at least the important ones, can be stored to disk and re-loaded.

4.2 The World's Best HSV Colour Picker
In examining a range of commercial HSV colour pickers I found strengths and weakness in them all, so I decided to build my own incorporating the best features and adding new ones, based on some of the design features outlined above. Fig. 6 shows how hue, saturation and value are linked, though independently modified. If the hue is changed, for example, the saturation bar shows all level of saturation from white to the pure hue, while the value bar will show the current saturation of the current hue, diminishing to zero (black). This arrangement overcomes the problem (for example) of trying to adjust just the saturation in an area-type representation of saturation and value, where one can easily change the value parameter as well.

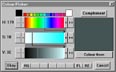Fig. 6 A new colour picker

4.3 Interfacing to the Voss Fractal
The Voss fractal texture generator uses approximately twenty parameters, so building a dialogue box for it required the use of more of the design principles outlined earlier than with the colour picker. Fig. 7 shows the dialogue box in its present stage of development, the main feature of which is the area devoted to the 'session', allowing the commenting and recall of each image with its parameter set, and the saving and loading of the entire session.

Fig. 7 The Voss fractal dialogue box

4.4 Case Study: RaySculpt
RaySculpt derives from a ray tracer written by my colleague Richard Wright, and a modeller based on spheres, originally known as 'Sculptor' [11]. RaySculpt provides for both arbitrary and algorithmic synthesis and modification of primitives. The colour picker, Voss fractal and marble texture generators are part of the system, as is the concept of 'hot buttons', which relates to the idea of a session. These buttons indicate the last eight menu commands issued to the system, in the form of 2 letter identifiers that are identical to their (Windows) keyboard shortcuts. These appear on every dialogue box, and also on the menu bar, which means that one can rapidly repeat a previous action. This is important in an exploratory mode: typically one needs to make a few adjustments to parameters and re-render the scene in a cyclical fashion. Fig. 8 shows the RaySculpt layout with various dialogue boxes. A single press on a hot button removes all dialogue boxes and allows, for example, a rendering or an adjustment of light position.

Fig. 8 RaySculpt screen layout